Route optimization with transfers possible?

Directions API Route Optimization API
1

Is it possible to model transfer relationships? In other words, where the algorithm calculates shipments with partial routes?

We have 500 origin-destination relations. However, these do not have to take place in a single route, but can be fulfilled with transfers over several routes.

Are there any tricks to model this? Or are there approaches to calculate this over several steps?

2

Do you have an example? With e.g. shipments and relations you could model more complex scenarios but I’m unsure about your requirements.

3

Real world example (simple one):

  • 40 shipments with different pickups but one destination/delivery

  • 3 vehicles

    • 50 seats
    • 25 seats
    • 25 seats

  • solution we get over the api:

    • 2 vehicles (25 and 25)
    • both have the same destination

  • solution we have in mind:

    • 2 vehicles (50 and 25)
    • but vehicle #1 meets vehicle #2 mid way and the persons transfer from #2 into #1
    • result: less km, but ca. 50% shipmens have a transfer (“Umstieg”) to reach their destination.
4

So something like this:

  1. you put 25 items into vehicle A (50) at location X (or 25 different locations x_i) and
  2. you put 25 items into vehicle B (25) at location Y (or 25 different locations y_i) and
  3. then at transfer point Z vehicle A gets all items of B and
  4. vehicle A delivers at final destination

?

Would there be more than a single meeting point? If no, do you know the meeting point in advance?

5

Yes, exactly. But it’s more complicated:

The background is that we have a static route with high capacity where the shipments might change into, but don’t need to.

We know the meeting points in advance, its the stops of the static route.

The difficulty is to determine which shipments are best to be transfered which are best to be transported directly.

6

The background is that we have a static route with high capacity where the shipments might change into, but don’t need to.

I’m unsure if I can follow. If they don’t change all into this “high capacity route” then the vehicle would have to go to the final destination even with just a single item (?)

Could you preprocess this using the Matrix API maybe?

7

We try to optimize public transport systems where some bus lines are static, but people can change into, other lines need to be “found”. We wan’t to model that a shipment can either be fulfilled in one route or by changing into a static route which also drives to the destination.

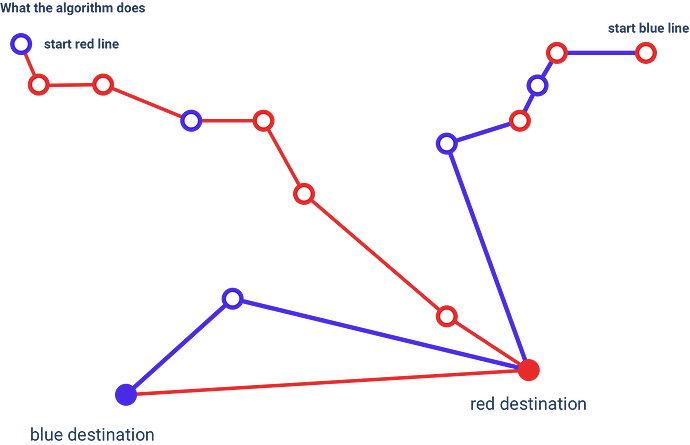
For example this constellation:

  • Let’s say the red line already exists, we can model it by relations.
  • But we want now, that the oder red pickup points make it to the red destination
  • And blue pickup points make their trip to the blue destination
  • The algorithm would model the red line, since we force it to by relations
  • but the other points are then transported in an own line to both destinations (picture 1).
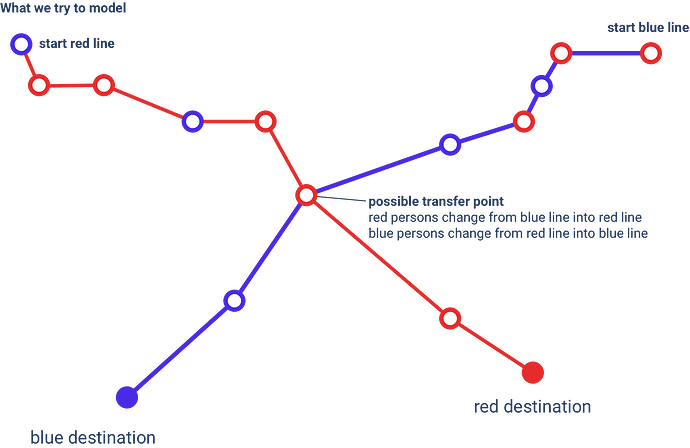
  • the better way would be to let them change the vehicle at the transfer point (picture 2)

image
image1566×1010 65.3 KB

image
image1554×1010 71.2 KB

Is it possible to do this by using the matrix API? Are any other approaches?

8

When you know the transfer point could you model this using two route optimization requests?

The first request is a delivery with two vehicles to the transfer point and the second request does the delivery from the transfer point (starting time is the latest arrival of the first response).

This way you won’t need relations and shipments.

9

yea, that’s the thing we try to avoid, that we set the transfer points manually. The transfer point can be any “bus stop” (Service, Pickup, Delivery) on the static route.

10

Even if you don’t set the transfer manually I think transfers are really tricky in logistics. Because what will happen if there is a single delay? Then both vehicles get this delay.

At the beginnings of GraphHopper I was at a ride sharing startup and we investigated if transfers would make sense. I.e. car A picks up a passenger and at location X the passenger would transfer to car B. I even found an algorithmic optimal solution (but only for two drivers and a single passenger that does the transfer) and the transfer point came out of this dynamically. But the real world requirements made this suboptimal. Is it always possible to find a practical safe transfer point for the theoretically found optimum? And should vehicle A wait for vehicle B? If yes, who pays for this? And if no, what if it rains or is cold? What if vehicle B never arrives?

But let’s say you solve this somehow, then why are there no blue points on the red line after the transfer point and no red points on the blue line after the transfer point? Isn’t the chance for something like this relative low for equally spread points? Or is it due to some business or geographical properties that the chance for this is high?

11

In terms of complexity in the “real world” you are totally right. Designing transfers is not an easy task, however they exists in public transport systems often.

The example from above is an easy one. In our scenarios we plan with a dozen routes and like 20 destination points.

That is also the reason why we try to figure out if a system with transfers could be cheaper than a system where you have multiple routes, sharing the same roads, picking up persons from the same bus stops but then heading to different destinations. We expect a smaller amount of routes/vehicles and a shorter total distance.

Currently this operation done manually by a customer of us and we are evaluating if we can help them.

12

Not sure if it helps but …

if you know the red line then you could calculate the blue line (ignoring the destination of its red items for a moment) and then you can calculate the overhead (additional time and distance) using the Matrix API for 5 different transfer points:

  • at the crossing X of blue and red line (no overhead, nothing to calculate, except they cross via tunnel and bridge but then you could just reject this point)
  • the last stop before the crossing X on the blue line (red line makes a detour)
  • the first stop after the crossing X on the blue line (red line makes a detour)
  • the last stop before the crossing X on the red line (blue line makes a detour)
  • the first stop after the crossing X on the red line (blue line makes a detour)

As you already know the distance and time from blue_before_X and blue_after_X you only need two matrix requests:

  • one 1x2 matrix request: blue_before_X to red_before_X and red_after_X
  • one 2x1 matrix request: red_before_X and red_after_X to blue_after_X
  • (you could expand this logic to more points)

There is one exception: when the crossing is before the last blue point on the red line but in that case you have the calculate the overhead once, i.e. for this blue point.

Afterwards you won’t need more requests but you would have to adjust the ETAs (or just do the route optimization requests in my earlier comment where the knowledge of the transfer point is required).

13

Okaay, we’ll try to play around with the matrix API. It seems that we need to implement a lot more logic to cover all possible usecases.