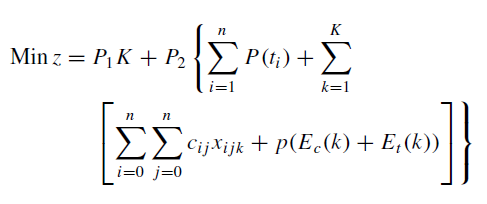Back to reducing the number of vehicles, I am not sure if I understand your points. As far as I can see, if one sets the fixed cost and the fixed cost param sufficiently large, wouldn’t minimizing the total cost equivalent to minimizing the number of vehicles first?
I think this is the usual way to deal with reducing the number of vehicles in the literature. For example, Fu et al. (2008) use the following objective function in their tabu search algorithm to evaluate the solutions, where K is the number of vehicles, the part inside the { } after P2 is the total deviation of time windows + the total travel distance + the infeasibility penalty, and P1 and P2 represent the priority levels (P1 >> P2). In this way, they are able to minimize the number of vehicles.