Hello! I’m trying to edit the algorithmConfig.xml to get a lower number of vehicles in the solution of VRPTW. I started from the xml configurations related to the VRPTW problem available in jsprit github webpage.
I’m working on Solomon istances and I used the SolomonReader class. I need to reduce the number of used vehicles, especially in RC instances. My idea was to introduce a FixedCost for each vehicle directly from the constructor of SolomonReader,
public SolomonReader(VehicleRoutingProblem.Builder vrpBuilder, double fixedCostPerVehicle)
but this way the number of vehicles did not decrease very much (it decreased for a maximum of one vehicle) and the total cost of the solution rose a lot.
I’ve also introduced the<considerFixedCosts weight="x.x">true</considerFixedCosts> in the xml configuration with many values of weight, but nothing changed.
How can I enforce the algorithm to use a lower number of vehicles without increasing too much the global total cost?
Thanks in advance.
Adding fixed costs automatically increases the overall costs. If you want to compare it with the Solomon instances, you need to subtract the fixed costs, i.e. minus number_of_vehicles * fixed_costs. But still, you might not end up with the best number of vehicles. The reason is that the algorithms in jsprit do not minimize the number of vehicles first and then the total variable transportation costs, but minimize variable transportation costs right from the beginning. Sometimes, however, these are competing objectives. Here, you can always try to build an approach yourself. For example, start with an infinite fleet. Solve the problem. Turn it into a problem of finite fleet and reduce the number of vehicles by one. Do this as long as you can just assign all customers. Then you definitely get better results in terms of number of vehicles employed. But still, there might be problems where you cannot find the best number of vehicles. Here, you probably need to find more appropriate ruin and recreate strategies.
I thought it will try to minimize the total cost, which is the transportation cost + the fixed cost in this case, no?
If so, wouldn’t it minimize the number of vehicles first if one sets the fixed cost sufficiently large?
Just wondering. Thanks.
Best regards,
He
He, you are correct. If you add fixed costs, it will be considered and the algorithm tries to reduce fixed costs also. However, the insertion heuristics in jsprit usually insert unassigned customers according to the lowest marginal insertion costs. If you add fixed costs then it tends to prefer solutions with less vehicles (in contrary to no fixed costs). This approach generally tends to provide you with solutions with less vehicles. However, there is no strategy yet that minimizes the number of vehicles explicitly. Adding this: <considerFixedCosts weight="x.x">true</considerFixedCosts> might help since it incorporates fix costs into the insertion process, but it only impacts the solution if there is the decision of using a new vehicle during insertion or not. Once you use a new vehicle, it does not have an effect anymore.
Thus, I think we should think about a new approach to explicitly minimize the number of vehicles first. Any thoughts on this?
To give an example. Just run this:
VehicleTypeImpl type = VehicleTypeImpl.Builder.newInstance("type").build();
VehicleImpl v = VehicleImpl.Builder.newInstance("v")
.setType(type)
.setReturnToDepot(false).setStartLocation(Location.newInstance(0,0)).build();
Service s1 = Service.Builder.newInstance("s1").setLocation(Location.newInstance(0,10)).build();
Service s2 = Service.Builder.newInstance("s2").setLocation(Location.newInstance(10,0)).build();
Service s3 = Service.Builder.newInstance("s3").setLocation(Location.newInstance(0,-10)).build();
Service s4 = Service.Builder.newInstance("s4").setLocation(Location.newInstance(-10,0)).build();
VehicleRoutingProblem vrp = VehicleRoutingProblem.Builder.newInstance().addJob(s1).addJob(s2).addJob(s3).addJob(s4)
.addVehicle(v).build();
VehicleRoutingAlgorithm vra = Jsprit.createAlgorithm(vrp);
VehicleRoutingProblemSolution s = Solutions.bestOf(vra.searchSolutions());
SolutionPrinter.print(vrp,s, SolutionPrinter.Print.VERBOSE);
new Plotter(vrp,s).plot("output/example.png","test");
This should yield: 4 vehicles and 840 costs
If slightly change the example by adding fixed costs and a fixed costs param like this:
VehicleTypeImpl type = VehicleTypeImpl.Builder.newInstance("type")
.setFixedCost(200)
.build();
VehicleImpl v = VehicleImpl.Builder.newInstance("v")
.setType(type)
.setReturnToDepot(false).setStartLocation(Location.newInstance(0,0)).build();
Service s1 = Service.Builder.newInstance("s1").setLocation(Location.newInstance(0,10)).build();
Service s2 = Service.Builder.newInstance("s2").setLocation(Location.newInstance(10,0)).build();
Service s3 = Service.Builder.newInstance("s3").setLocation(Location.newInstance(0,-10)).build();
Service s4 = Service.Builder.newInstance("s4").setLocation(Location.newInstance(-10,0)).build();
VehicleRoutingProblem vrp = VehicleRoutingProblem.Builder.newInstance().addJob(s1).addJob(s2).addJob(s3).addJob(s4)
.addVehicle(v).build();
VehicleRoutingAlgorithm vra = Jsprit.Builder
.newInstance(vrp)
.setProperty(Jsprit.Parameter.FIXED_COST_PARAM, "2.")
.buildAlgorithm();
VehicleRoutingProblemSolution s = Solutions.bestOf(vra.searchSolutions());
SolutionPrinter.print(vrp,s, SolutionPrinter.Print.VERBOSE);
new Plotter(vrp,s).plot("output/example.png","test");
It yields 1 vehicle and 252.426 costs. So here, adding fixed costs and this parameter that considers fixed costs within the insertion make the difference.
Oh no, I only for the first time realize that Jsprit algorithm does not by default consider fixed cost. Without this line, fixed cost won’t work. I need to revisit my soft time window codes…
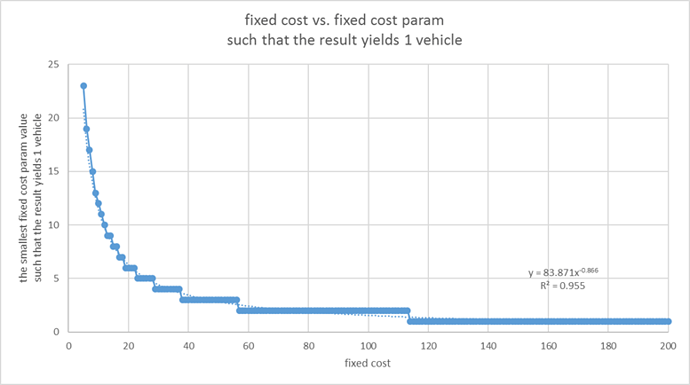
I played around with your example, especially with the fixed cost and the fixed cost param. Theoretically, when the fixed cost is larger than 4, the result should yield 1 vehicle and total cost of 52.426 + fixed cost; however, the fixed cost param needs to be sufficiently large for this to happen. For example, if the fixed cost is set as 5, then, only when the fixed cost param is larger than 22 (I only tested with integer values here and after), the result will yield 1 vehicle; on the other hand, if the fixed cost param is set as 1, then, only when the fixed cost is larger than 113, the result will yield 1 vehicle.
The figure at the end shows the result, in which the x-axis is the fixed cost and the y-axis is the smallest fixed cost param value such that the result yields 1 vehicle.
I wonder what role the fixed cost param plays here? Why does it have to be sufficiently large such that the fixed cost can force the result to yield 1 vehicle in the example?
Thanks.
Best regards,
He
Back to reducing the number of vehicles, I am not sure if I understand your points. As far as I can see, if one sets the fixed cost and the fixed cost param sufficiently large, wouldn’t minimizing the total cost equivalent to minimizing the number of vehicles first?
I think this is the usual way to deal with reducing the number of vehicles in the literature. For example, Fu et al. (2008) use the following objective function in their tabu search algorithm to evaluate the solutions, where K is the number of vehicles, the part inside the { } after P2 is the total deviation of time windows + the total travel distance + the infeasibility penalty, and P1 and P2 represent the priority levels (P1 >> P2). In this way, they are able to minimize the number of vehicles.
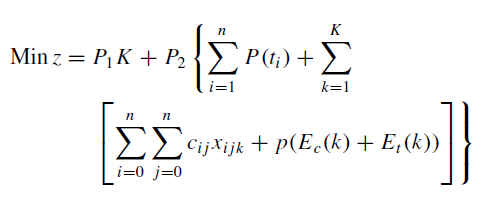
He, thanks a lot for your analysis. This is great and it really helps all to understand the functioning better. I assume that the example I gave is too artificial to draw valuable conclusions for bigger problems. We should better use the Solomon instances (e.g. RC*) or the instances from Christofides, Mingozzi and Toth. There are also instances and according readers in jsprit-instances. As you will see if you solve RC1 instances, it makes a difference whether you set fixed costs or not (even without setting the fixed_cost_param). Thus, if you set the fixed costs, they are included in the objective funtion automatically and thus solutions are preferred with less vehicles. However, there are no explicit search strategies that solely try to find areas in this huge search space with less vehicles. It is always a combination of finding areas that reduces variable costs, and this very often comes with less vehicles. This brings me back to the RC1* instances from Solomon, very often you end up with a good solution when it comes to the variable costs, however in many instances, the algorithm does not find the best number of vehicles. However, if you set the best number as fixed and specify a vrp with finite fleet, in almost every case you come close to the best known solution. So we need to find ways that does this automatically, i.e. without setting the best number of vehicles manually. So this is an interesting, but challenging task :), and doable - I think. Will think about it further, and really appreciate any thoughts on this.
Thanks again for your valuable analysis!
Thank you very much to stefan and jie31best! I really appreciated your contributes. I’m thinking about this problem yet. I’ve done many tests with Solomon instances trying to adapt your code and I’ve seen that in some cases the number of vehicles drops down significantly by setting high fixed cost for vehicles but in other cases the changes are very little. Globally I’ve not found a solution that minimize the total cost and, at the same time, the number of vehicles. If I’ll find any ideas I’ll update this topic.
Thank you very much for the help!
Let us know your findings. Thank you for triggering this discussion :).
Does anyone have any news on how to reduce the number of vechicles? I’ve tried using fixed costs but the results won’t change.
I mean, in the instance I’m running all the services can be visited with 1 vehicle, but if I add more than 1 vehicle, like 2 or 3, it will use all of them.
In my scenario using less vehicles is the first variable for a reduced cost.
@stefan, is creating a new ruin and recreate strategy the proper way to solve this ? Any advices?
Thanks