Inconsistent points between matched trips which cross the same road segments

[pcingi]

I work for for wecity - a mobile app which rewards sustainable mobility - and I’m using the map-matching tool for performing various types of data analysis on the trips performed, recorded and uploaded by the users.

One of the most frequent analysis I perform concerns answering the question “which road segments (of the OSM graph of a city) are crossed more frequently?”

The approach I use is roughly this:

1. • I receive sets of “raw” GPS points (subject to error, thus in general not laying on any OSM edge), each of them representing a trip performed by a user.
2. • I use a python script (which sends a map-match request to my locally hosted graphhopper) to convert such trips into sequences of points that are actual nodes of the OSM graph
3. • The same python script converts the sets of map-matched points to sets of edges (by aggregating subsequent points : each edge is intended as an unordered set of two points), and store them into a postgis database.
4. • I use spatial queries for grouping the records by edge, and counting how many times every single edge appears (note that given the fact that edges are stored as unordered sets of points, the grouping is not sensitive to the orientation. E.g. edges [1,2] and [2,1] will result as the same edge for concerning grouping and counting).

The analysis runs successfully but I noticed that in some areas of the I had different overlapping edges laying on the same road segment, making the crossings count ambiguous and inaccurate for these minor parts of the graph.

I thought that this was due to response simplification: some of the points resulting from the map-match are indeed discarded as long as 1. their removal does not affect the resulting trip shape too much and 2. they are not junction nodes. This seemed plausible as the map matching processes of two trips which overlap in some parts may choose to remove different sets of points during the simplification due to the differences in the “overall” shape of the two trips.

I managed to disable the simplification. Nonetheless, the results were not quite as expected. After disabling the simplification my map-matched trips database contained approx. 6 000 000 lines (one line for each edge that was crossed in one of the map-matched trips) - that’s reasonable, it resulted in 4 500 000 lines before - but after the grouping it only reduced to 2 600 000 unique edges, while when the simplification was allowed the unique edges resulted to be only 100 000. Things are significantly worse this way.

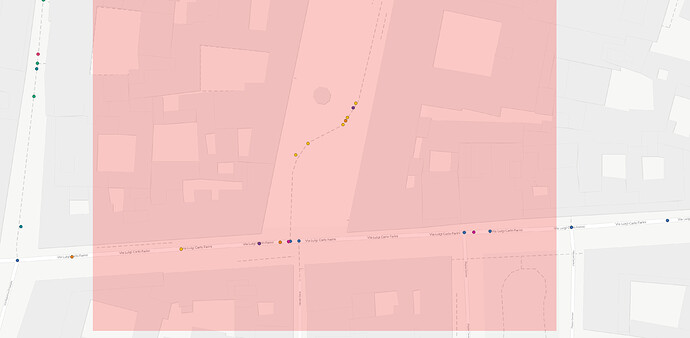
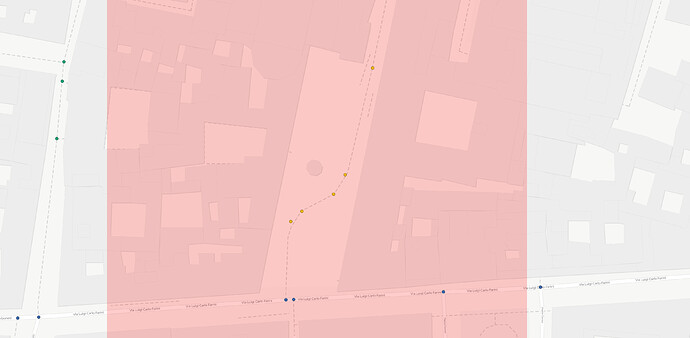
To investigate the issue, I plotted the map-matched nodes from 10 trips that overlap in some parts in order to check if the map- matching process returned the same nodes when suggesting the same path. This is what I obtained (I suggest to use the link, the popups help understanding the map content which is hard to explain with a static image):

Simplification disabled:

Simplification allowed:

As an example, I’ll refer to the small stretch of cycleway highlighted in the images above. Such path is crossed by three trips, of ids 3, 5 and 8. It is a relatively isolated path, so it is sure enough that all the three map-matched trips should point to the very same osm way. Disabling the simplification adds one additional point to every one of these trips, but these additional points do not coincide.

Therefore I’m confused. Having disabled the simplification, shouldn’t I obtain all the nodes that are present on the path in all the three cases? I.e. should’t three trips result in the very same nodes on that part?

Thank you,
Pietro

[easbar]

I’m not sure why the different trips do not result in the very same nodes. However, I also wonder if the approach you are using to determine how frequently a given road segment is crossed is ideal. Instead of creating your own ‘edges’ out of pairs of subsequent points why don’t you use the GraphHopper edge IDs? GraphHopper already assigns a unique number to each edge (a road segment between two junctions) and to me it seems like all you need to do is count how many times each edge appears in your matched trips. You should try setting traversal_keys=true for your map matching requests which will give you the ‘edge keys’ for all edges of the matched trip. An edge key encodes the unique edge ID and the direction of an edge. To get the edge ID simply divide the edge key by two and round to the next lower integer (e.g. 4/2=2, 3/2=1).

[pcingi]

Thank you so much for the hint! Actually I already tried to go that way by adding “details=edge_id” to the request: it seems this yelds the actual edge id, i.e. the result of floor(edge_key/2.0), and has the advantage of having each id associated to a set of map-matched points.
I stopped those tries because I was not able to find a good way to represent the edge associated to a graphhopper ID on a map (this would require the coordinates of its points).

Maybe I could still keep the geometries (couples of subsequent points), group&count according to their edge_id, and then use the union of all the geometries sharing the same edge_id to represent each road segment on the map.

[easbar]

@pcingi

I stopped those tries because I was not able to find a good way to represent the edge associated to a graphhopper ID on a map (this would require the coordinates of its points).

Ok, but this is very easy using the Java API, or otherwise you could also add your own server endpoint to get this information per edge id.

[pcingi]

Ok, the second option sounds really good! I’ll try to go that way.

In the meantime I managed to implement the grouping by edge id, and it works definitely better. My only worry is: how much do graphhopper edge ids change each time the graph is regenerated with a newer version of the .osm.pbf file?
I may mind this because I store the map-matched data in a database that keeps growing, and I use that database to create maps on demand. A few time per year I pause the map-matching process, update the GH graph, and resume the process (this was no big deal as long as I grouped based on geometry, it might be now).

[easbar]

@pcingi

Ok, the second option sounds really good! I’ll try to go that way.

And of course you could also modify the map matching endpoint to return not only the edge IDs, but also the coordinates of the associated points.

@pcingi

I may mind this because I store the map-matched data in a database that keeps growing, and I use that database to create maps on demand. A few time per year I pause the map-matching process, update the GH graph, and resume the process (this was no big deal as long as I grouped based on geometry, it might be now).

Yes, the edge IDs will change when you do imports with different versions of the OSM data, so this will indeed be a problem. Maybe you can use the edge ID for the groupings, but then generate your own IDs based on the coordinates of the corresponding nodes to identify edges between different OSM updates.