Hi, thought I would update my solution for solving this.
Essentially it all boiled down to setting costs in the costMatrix and building specific relations only.
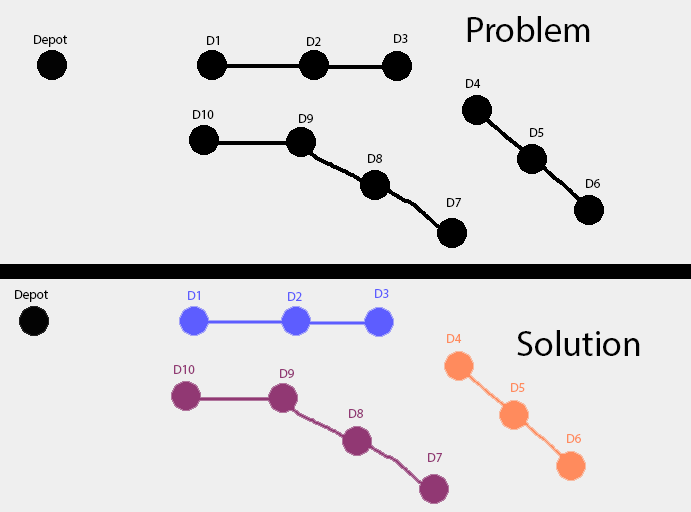
For three points we want to constrain to the given sequence so;
Home, A, B, C
We build Home -> A, Home -> B, Home -> C : This is because we might need more than 1 vehicle to complete the deliveries.
Then A -> B, B-> C is produced by graphhopper.
A -> C etc is set at 99999999.0 distance / time.
// Build the depot relations
for (int i = 1; i <= vrpBuilder.getAddedJobs().size(); i++){
// We want to add depot to first location for every point, Distance is temp removed at moment
Pair<Double, Double> distancesFromDepot = pointToPointDistance(getDepotLocation.getX(), getDepotLocation.getY(), listOfPoints.get(i-1).getLatitude(), listOfPoints.get(i-1).getLongitude(), Double.parseDouble(jTextField4.getText()));
costMatrixBuilder.addTransportTime("0", String.valueOf(i), distancesFromDepot.getValue());
Pair<Double, Double> distancesToDepot = pointToPointDistance(listOfPoints.get(i-1).getLatitude(), listOfPoints.get(i-1).getLongitude(), getDepotLocation.getX(), getDepotLocation.getY(), Double.parseDouble(jTextField4.getText()));
costMatrixBuilder.addTransportTime(String.valueOf(i), "0", distancesToDepot.getValue());
}
// Single thread process that does work
for (int i = 1; i <= vrpBuilder.getAddedJobs().size(); i++){
for (int j = 1; j <= vrpBuilder.getAddedJobs().size(); j++) {
if(i+1 == j){
Pair<Double, Double> distances = pointToPointDistance(listOfPoints.get(i-1).getLatitude(), listOfPoints.get(i-1).getLongitude(), listOfPoints.get(j-1).getLatitude(), listOfPoints.get(j-1).getLongitude(), Double.parseDouble(jTextField4.getText()));
costMatrixBuilder.addTransportTime(String.valueOf(i), String.valueOf(j), distances.getValue());
}else{
costMatrixBuilder.addTransportTime(String.valueOf(i), String.valueOf(j), 99999999.0);
}
}
}
With a fleet set as INFINITE we should get a solution which provides the number of vehicles. Issue is JSprit will use an extra vehicle to limit cost of travel, so the solution generally will never have the minimum number of vehicles required.
So you can either perform checks to select solutions with smallest vehicle numbers and more cost, or as we have a constrained sequence, not use JSprit at all and only use Graphhopper.
So we build the relations between each point still and then manually assign the deliveries to each van;
Relations for each DP : Distance/Time from home, distance/time to next DP, distance/time back to home, service time.
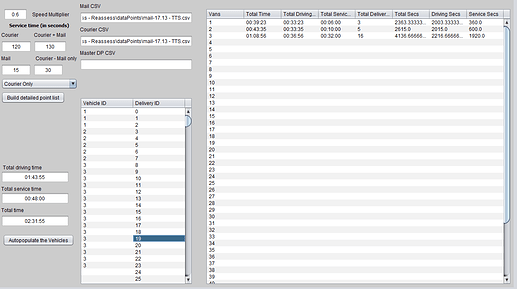
From there we can set the vehicle ID to each DP until we reach the cap (in this case I wanted 8 hours per vehicle)
Here is the snippet.
As you start assigning vehicles the solution is calculated.
From there I used an autopopulate to assign each delivery, then check to see if the total time is >8 hours. If it is, move to the next vehicle.
That was the solution I came up with any hows. It takes ~10 minutes to process 8000+ deliveries.